Gaussian Free Field 2015

Lecturers: Prof. Dr. Anita Winter & Dr. Anton Klimovsky
Time & location: Tuesday, 10:15-12:00 @ S-U-3.03
Begin: April 7
Frequency: 2 hours/week
Target audience: Master-level math
Pre-requisites: Probability Theory II (WT II)

Description


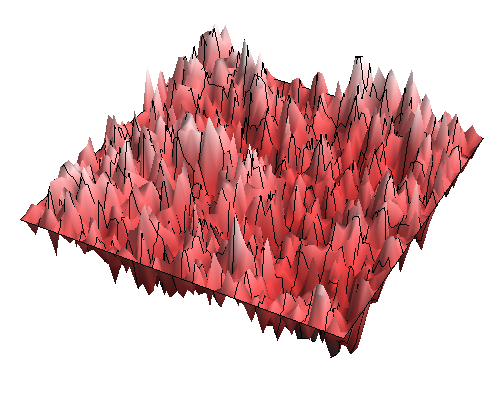
A realization of discrete GFF on a square grid $60 \times 60$

Brownian motion is a centered Gaussian Markov process $ W = { W(t) }_{t \in I} $ indexed by the half-line $I := [0,+\infty)$ and having stationary independent increments. We think of $I$ as of the time line along which Brownian motion evolves. Alternatively, to define Brownian motion, we could have just postulated that $W$ has the covariance $\mathbb{E} [ W(t) W(s)] = t \wedge s$ for all $t, s \in I$. (We require that $W(\cdot)$ is a.s. continuous.)

Often, complementary to processes evolving in time, we want to model spatial processes, where to each point in space, say $x \in \mathbb{R}^2$, we attach a real random variable $h(x)$. (As an example, one can think, e.g., of the temperature distribution on a planar surface). Such spatially indexed collections of random variables $ { h(x) }_{x \in I}$ are called random fields. In the case $I = \mathbb{R}^2$, we can visualize the random field as a random surface in $\mathbb{R}^3$, where $h(x)$ is the height (or depth, if negative) of the surface at point $x \in I$ above (below) the reference level $0$. (See the above picture.)

Gaussian free field (GFF) is a generalization of Brownian motion to such spatially indexed settings. Similarly to Brownian motion, GFF is a centered Gaussian process which satisfies a spatial generalization of the Markov property -- the Gibbs-Markov random field property. Apart from that, GFF is tightly linked to the behavior of random walks on graphs: the covariance of GFF is given by the inverse graph Laplacian. Given this, it is not surprising that GFF is an important probabilistic object which has recently received much attention in the mathematics literature.

In this course, we shall present the main results currently available on the behavior of GFF together with the tools that are used to study these objects. Specifically, we will learn about

  • Gaussian processes indexed by general index spaces;
  • Spatial behavior of random walks on graphs: local times, potential theory, Green's function, Dynkin's isomorphism;
  • Time-permitting: Extreme-value theory: point processes, extremal distributions, extremal processes.

Literature

Lecture notes and reviews:

Concentrated seminar

Takes place on October, 1st, 2015.

Schedule:

  • 10:15 Begin.
  • 2 Talks
  • 12:00-13:30 Lunch
  • 2-3 Talks

1 Talk = 50 minutes.

Seminar topics:

  • Biskup and Louidor. "Extreme local extrema of two-dimensional discrete Gaussian free field." (2013). [pdf] Anton Klimovsky
  • Bolthausen, Deuschel and Zeitouni. "Recursions and tightness for the maximum of the discrete, two dimensional Gaussian Free Field." Electron. Commun. Probab 16 (2011): 114-119. [pdf] Erik Wellner
  • Chiarini, Cipriani, and Hazra. "A note on the extremal process of the supercritical Gaussian Free Field." (2015). [pdf]
  • Ding, Lee and Peres. "Cover times, blanket times, and majorizing measures." (2011). [pdf] Anita Winter + Fabian Gerle
  • Eisenbaum. "Inequalities for permanental processes." Electron. J. Probab 18.99 (2013): 1-15. [pdf]
  • Subag and Zeitouni. "Freezing and decorated poisson point processes." Communications in Mathematical Physics 337.1 (2015): 55-92. [pdf] Tim Schönberger